|
|
|
| Das Sagnac-Experiment - die klassische Beschreibung | |
|
|
|
| Der Sagnac-Effekt bildet die physikalische Grundlage der optischen Kreisel die in der Form als Glasfaserkreisel oder Laserkreisel in der autonomen Navigation den klassischen mechanischen Kreisel teilweise abgelöst haben. | |
| - zurück zur Startseite - nächstes Kapitel - vorheriges Kapitel |
|
| In dieser Einführung geht es nicht um die technische Realisierung dieser modernen optischen Kreiselgeräte, sondern um einige Fragen die für die Anwendung des Sagnac-Effektes von grundsätzlicher Bedeutung sind, die in der Standardliteratur zu diesem Thema aber meist zu kurz kommen:
- reagiert der optische Kreisel wirklich nur auf Dreh- und nicht Translationsbewegungen ? In einem weiteren Kapite soll die Frage angesprochen werden, ob der Sagnac-Effekt ein relativistischer Effekt ist, oder ob er mit den Mitteln der klassischen (vorrelativistischen) Physik beschrieben und verstanden werden kann ? |
|
|
Diese Themen werden uns in den nächsten Kapiteln beschäftigen , - als Einstieg werden wir uns aber zunächst mit der rein klassischen Beschreibung beschäftigen, - sozusagen den Standpunkt von Georges Sagnac einnehmen: |
|
 |
Georges Sagnac 14.10. 1869 (Perigeux) - 26.2. 1928 Arbeiten auf den Gebiet der Röntgenstrahlung und zur Ausbreitung von Licht in rotierenden Systemen. (mehr) Über Georges Sagnac ist ansonsten wenig bekannt, insbesondere habe ich kein Bild von ihm gefunden; ersatzweise finden Sie links eine von Sagnac angefertigte Skizze seines Interferometer. |
| Der Fairness halber sollte erwähnt werden, dass ein ähnliches Experiment von Franz Harress zwischen 1909 und 1911 - also noch vor Sagnac - durchgeführt wurde. Seine Messergebnisse wurden aber erst 1920 von Max von Laue richtig interprtiert. (mehr) | |
| Sagnac interessierte sich für die Frage wie sich Licht in rotierenden Systemen verhält; seine Experimente können durchaus als Pendant zum den Michelson-Experimenten gesehen werden, der sich für den Einfluß einer gleichförmigen, geradlinigen Geschwindigkeit auf die Ausbreitung des Lichtes interessierte. | |
| Auch wenn die Gegener der Relativitätstheorie das Gegenteil behaupten: Im Kapitel "Laufzeiteffekte in relativ bewegten Systemen" werde ich Ihnen zeigen wie sich die Ergebnisse von Michelson und Sagnac problemlos miteinander "versöhnen" lassen ! |
Die Ergebnisse beider Experimente sind im Zusammenhang gesehen ein hervorragendes Indiz für die Richtigkeit der Relativitätstheorie, - aber dazu später mehr! |
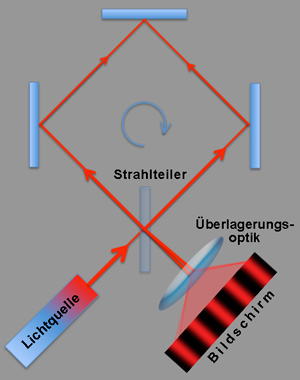
| Der Versuchsaufbau den Sagnac für seine Untersuchungen benutzte - insbeondere die Skizze dazu (oben links) - ist etwas unübersichtlich; deshalb hier eine (hoffentlich) etwas einfachere Prinzipskizze. | |
| Ausgehend von einer Lichtquelle (heutzutage ein Laser) trifft ein Lichtstrahl auf einen Strahlteiler; die Teilstrahlen durchlaufen in entgegengesetzter Richtung die Spiegelanordnung und werden nach einem Umlauf am Strahlteiler wieder ausgekoppelt und zu einem Interferenzstreifenmuster überlagert. |
 |
|
|
|
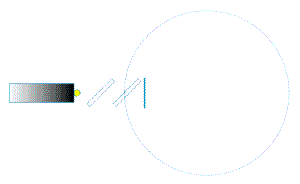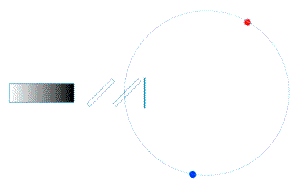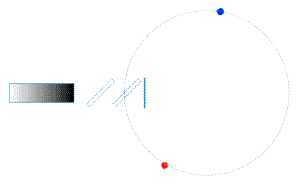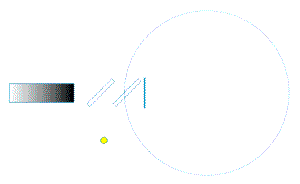
| Hier noch einmal eine etwas andere Darstellung mit einer kreisrunden Lichtleiterschleife, - in dieser Darstellung lässt sich anschliessend leichter rechnen !!! | |
| In dieser Anordnung durchläuft das Licht (hier dargestellt durch eine kleine gelbe Kugel) zunächst einen teildurchlässigen Spiegel, trifft dann auf einen Strahlteiler; dort wird es aufgeteilt (blaue und rote Kugel) läuft durch das kreisrunde Lichtleitersystem, wird nach einem Umlauf wieder ausgerkoppelt und schliesslich am ersten teildurchlässigen Spiegel überlagert.
Wenn alles richtig eingestellt ist, haben die beiden Lichtstrahlen nach einem Umlauf exakt den gleichen Laufweg hinter sich. |
 |
| Uns interessiert nun die Frage, ob durch eine Drehbewegung eine Änderung des Laufweges zwischen den gegensinnig umlaufenden Lichtwellenzügen hervorgerufen wird.
In der Animation könnte das so aussehen: |
|
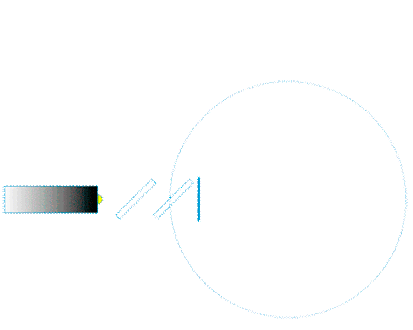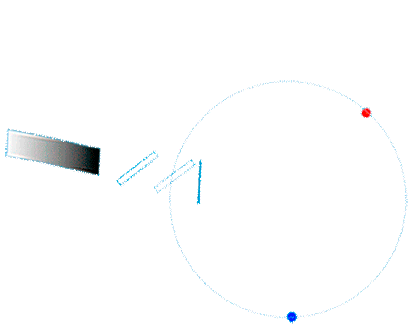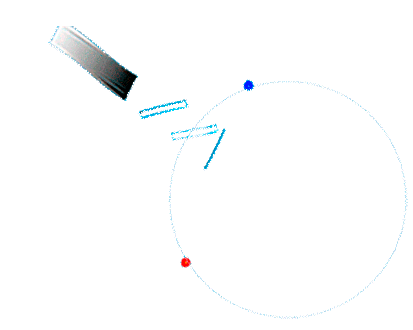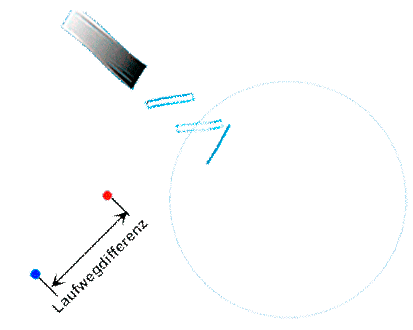 |
|
|
Um es gleich vorwegzunehmen - diesmal stimmt die Animation, bzw. die Erwartung der Physiker mit dem Ergebnis des Experimentes überein ! |
Sie erinnern sich ?
Eine ähnliche Animation hat uns beim Michelson-Interferometer schon einmal im Stich gelassen ! |
| Keine Angst - die Rechnung für beliebige Formen und beliebige Drehpunkte schauen wir uns auch noch an. Eines nach dem andern! |
Um die Angelegenheit für die Rechnung etwas einfacher zu machen, nehmen wir zunächst an, dass das Lichtführungssystem (Lichtleitersystem!) kreisrund ist und der Drehpunkt exakt im Zentrum liegt. |
| Das Gerät rotiert mit der Winkelgeschwindigkeit
|
|
| In diesem ringörmigen Lichtführungssystem lassen wir nun einen Lichtwellenzug einmal in Drehrichtung und einmal gegen die Drehrichtung umlaufen. | |
| - zurück zur Startseite - nächstes Kapitel - vorheriges Kapitel |
|
|
................
 ..................... .....................  |
|
|
..................Lichtwellenzug in Drehrichtung .................................................................Lichtwellenzug entgegen der Drehrichtung
|
|
| ... und jetzt läuft die Rechnung ganz ähnlich wie bei Michelson-Interferometer: | |
|
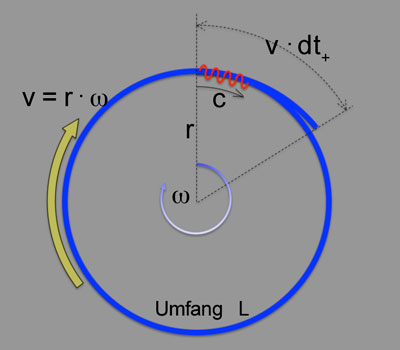
Der Lichtwellenzug durchläuft den ringförmigen Lichtleiter mit der Geschwindigkeit c.
|
|
| Zunächst der Lichtwellenzug in Drehrichtung (linke Skizze) : |
Während der Wellenzug das Lichtleitersystem einmal in Drehrichtung umrundet (linke Skizze), hat sich das Lichtleitersystem um die Strecke v.dt+ weiterbewegt, d.h. er muß die Gesamtstrecke
|
|
L+ = L + v.dt+ = c . dt+
|
|
| zurücklegen. Daraus ergibt sich für die Laufzeit des Lichtwellenzuges in Drehrichtung dt+ : | |
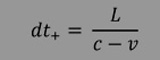 |
|
| ... und jetzt der entgegengesetzt umlaufende Wellenzug (rechte Skizze): |
Dem entgegengesetzt umlaufenden Wellenzug (rechte Skizze) bewegt sich die Anordnung entgegen; während der Umlaufzeit dt- hat sich das Lichtleitersystem um die Strecke v . dt- bewegt; der gesamte Laufweg verkürzt sich von L auf :
|
|
L- = L - v.dt- = c . dt-
|
|
|
Daraus folgt für die Laufzeit des Lichtwellenzuges in entgegengesetzter Richtung:
|
|
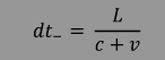 |
|
| Das ist gaaaanz wichtig ! Ich komme darauf zurück. | Bereits an dieser Stelle wird die enge Verwandtschaft zwischen dem Michelson- und dem Sagnac-Interferometer deutlich (zumindest aus der Sicht der klassischen Physik !); die Ausdrücke für die Laufzeiten dt+ und dt- im Sagnac-Interferometern und in dem Arm des Michelson-Interferometers, das parallel zu der zu messenden Geschwindigkeit liegt, sind vollkommen identisch !
Beim Michelson-Interferometer mußten wir die beiden Laufzeiten ( Hin- und Rückweg) addieren um sie mit der Laufzeit im zweiten dazu senkrechten Arm vergleichen zu können, - beim Sagnac-Interferometer können wir die Laufzeiten der beiden gegensinnig umlaufenden Wellenzüge direkt mit einander vergleichen und bilden deshalb die Differenz : |
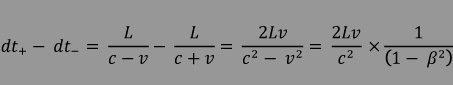 |
|
| mit : |
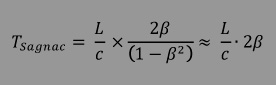 |
|
|
|
| Zwischenbemerkung ! | Sie erinnern sich ? Beim Michelson-Interferometer mußten wir mit einem Laufzeitunterschied von
Mit c = 300 000 km/sek (Lichtgeschwindigkeit) und v = 30 km/sek (Geschwindigkeit der Erde auf ihrer Umlaufbahn um die Sonne) ergibt sich |
|
|
|
| - zurück zur Startseite - nächstes Kapitel - vorheriges Kapitel |
Zur Auswertung des Laufzeiteffektes beim Sagnac-Interferometer verfährt man ganz ähnlich wie beim Michelson-Interferometer:
- nach einem Umlauf koppelt man die Lichtwellenzüge aus und überlagert sie; das dabei entstehende Interferenzstreifenmuster zeigt die Laufzeitdifferenz in Form einer Laufwegs- bzw. Phasenverschiebung an. |
Unter Berücksichtigung von 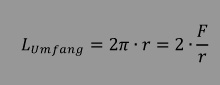 ergibt sich aus der obigen Beziehung für die Laufzeitdifferenz TSagnac : ergibt sich aus der obigen Beziehung für die Laufzeitdifferenz TSagnac : |
|
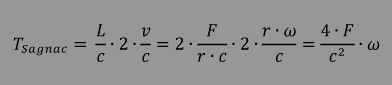 |
|
| wenn man nun noch den Zusammenhang zwischen Lichtgeschwindigkeit, Frequenz und Wellenlänge |
|
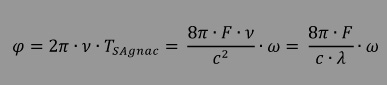 |
|
| d.h. wenn das Sagnac-Interferometer in eine Drehwegung versetzt wird, dann verschiebt sich das Interferenzstreifenmuster um den festen Wert proportional zu Drehrate. | |
| Für die "Navigationsexperten" unter Ihnen:
Das Sagnac-Interferometer, z.B. in der Form eines Glasfaserkreisels liefert eine Information über die Drehgeschwindigkeit Verwendet man den Sagnac-Effekt in einem optischen Ringresonator - das Ding nennt sich dann "Laserkreisel" - dann erhält man ein Ausgangssignal proportional zum Drehwinkel - das wird in der einführenden Literatur oft verwechselt! (Aber der Laserkreisel ist hier nicht unser Thema.) |
Lassen Sie uns ein Beispiel berechnen:
Fläche des Rininterfrometers F = 1 m2 ... ergibt für die Phasenverschiebung ziemlich genau 180o, d.h. das Interferenzstreifenmuster verschiebt sich um eine halbe Streifenbreite von hell nach dunkel. Für Drehgeschwindigkeiten die für die Navigation von Interesse wären, also z.B. die Erddrehrate mit 15 o/h wäre bei den oben genannten Abmessungen eine Phasenverschiebung von 8,75.10-5o zu erwarten; d.h. für solche Anwendungen müsste die Interferometerfläche F noch deutlich größer gemacht werden, was mit modernen Lichtleitfasern, aufgewickelt auf einer Spule, möglich sein dürfte. |
|
|
|
| Uff das war etwas "mühsam", aber eigentlich trivial - oder ?
Aber das eigentlich bemerkenswerte an diesem Ergebnis - im Gegensatz zum Michelson-Interferometer tut uns das Sagnac-Interferometer den Gefallen, dass das Experiment unsere "Trivial-Rechnung" exakt bestätigt ! |
|
|
|
|
| Ein naheliegendes Argument zur Eklärung für die Diskrepanz der Ergebnisse wäre, daß es sich beim Sagnacversuch (Rotation) um eine beschleunuigte Bewegung, beim Michelson-Experiment um eine nicht beschleunigte, gleichförmige Bewegung handelt. A. Sommerfeld bemerkt dazu (Vorl. über theoretische Physik, Bd.IV, S.67), "Wenn man beachtet, dass es sich bei den Versuchen (von Sagnac) nur um Geschwindigkeiten v<<c und nur um Effekte von erster Ordnung in v/c handelt, kann man ... einfach klassisch rechnen." | Ich weiß nicht wie es Ihnen geht? - Ich habe bei der Betrachtung dieser Resultate ein ganz schlechtes Gefühl !
Wir haben sowohl beim Michelson-Experiment als auch beim Sagnac-Experiment Signallaufzeiten berechnet. Im ersten Fall wurde die Signallaufstrecke geradlinig und gleichförmig mit der Geschwindigkeit v bewegt, im zweiten Fall handelte es sich um die Umfangsgeschwindigkeit v eines rotierenden Systems. In beiden Fällen handelte sich sich um eine Art "Wettrennen" zwischen dem Signal (=Lichtwellenzug) und einem bewegten Ziel ! Die Rechnungen dazu waren in beiden Fällen nahezu identisch. Trotzdem sind die experimentellen Ergebnisse so unterschiedlich wie nur möglich - im ersten Fall ein Nullresultat, im zweiten Fall vollständige Übereinstimmung zwischen Rechnung und Experiment ! Da bleibt nur eine Schlussfolgerung: Wir haben etwas Fundamentales übersehen ! Und wenn unsere Rechnung nicht mit dem Ergebnis des Michelson-Experiment übereinstimmt, dann muß auch die Rechnung zum Sagnac-Experiment falsch sein , denn unser Grundansatz ist hier genau der gleiche ! |
| Der Vollständigkeit halber muß erwähnt werden, dass Michelson in seinen ersten Experimenten tatsächlich einen kleinen Effekt beobachtet hat, der allerdings 20mal kleiner war als erwartet.
(Bei den späteren unzähligen Wiederholungen des Experimentes konnte man diesen Resteffekt immer weiter reduzieren, so dass es sich wohl doch nur um einen Messfehler handelt. mehr) Aber selbst wenn man - wie die Relativitätskritiker - annimmt, dass es sich dabei nicht um einem Messfehler handelt, dann muß immerhin erklärt werden, wieso das Meßergebnis so deutlich von der Rechnung abweicht. |
Ich weiß, - die Gegner der Relativitätstheorie argumentieren genau anders herum, nach dem Motto : was beim Sagnac-Experiment zum richtigen Ergebnis führt, kann beim Michelson-Experiment nicht falsch sein ! (Hier geht's zu den Relativitätskritikern.) |
| Ich glaube wir müssen das ganze Thema noch einmal völlig neu aufrollen und wir sollten dabei sehr genau auf die Randbedingungen achten ! | |
| - zurück zur Startseite - nächstes Kapitel - vorheriges Kapitel |
Bitte verstehen Sie mich nicht falsch: ich habe kein Interesse mich in den Streit um die Relativitätstheorie einzumischen. Ich möchte lediglich eine "saubere" Beschreibung des Sagnac-Effektes abliefern und einige damit verbundene Fragen untersuchen, deren Beantwortung mit der traditionellen, hier vorgeführten Rechnung kaum möglich ist:
Z.B. ist der Sagnac-Effekt: |

