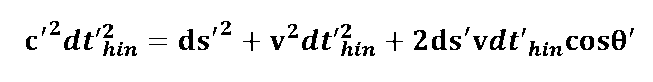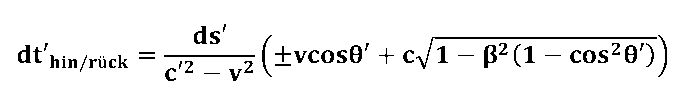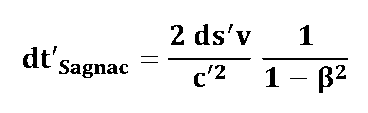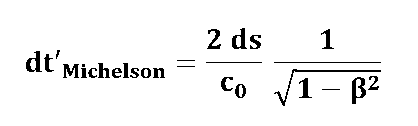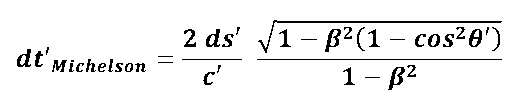Laufzeiteffekte in relativ bewegten Systemen-Vorüberlegungen

Laufzeiteffekte in relativ bewegten Systemen - Vorüberlegungen
Das ist nun das entscheidende Kapitel in dem wir den Sagnaceffekt etwas vollständiger beschreiben wollen, als das in der Literatur üblich ist.

Startseite vorheriges Kapitel nächstes Kapitel	Wir werden jetzt endlich (!) eine widerspruchsfreie Erklärung für die Resultate des Michelson- und des Sagnacexperimentes erhalten. Wir werden die Frage beantworten können, welche Rolle die Signalgeschwindigkeit spielt, ob ein dezentraler Drehpunkt den Messeffekt beim Sagnacinterferometer verfälscht und vielleicht das Problem lösen, ob der Sagnac wirklich ein "reinrassiger" relativistischer Effekt ist ? Zunächst müssen wir dazu etwas theoretische Vorarbeit leisten, - aber keine Angst - sie brauchen nicht mehr Mathematik als bisher, wir werden uns lediglich etwas genauer die Bewegungsrichtungen des Signals (z.B. Lichtwelle) und des Gesamtsystems (Interferometer) ansehen !
	Wir hatten bislang immer angenommen, das die Bewegungsrichtung des Signals im jeweiligen Interferometerarm genau parallel, bzw. senkrecht, zur Bewegungsrichtung des Gesamtsystems verläuft, so wie hier im Michelsoninterferometer :
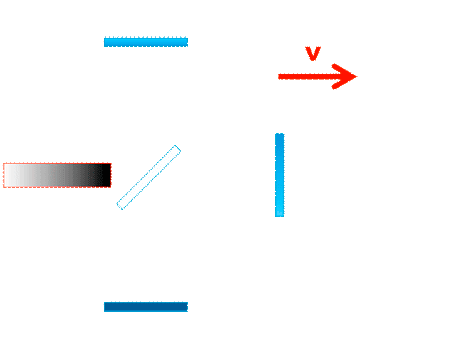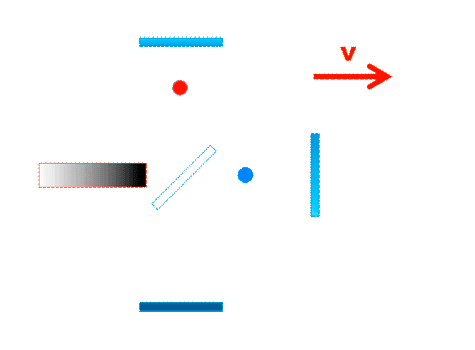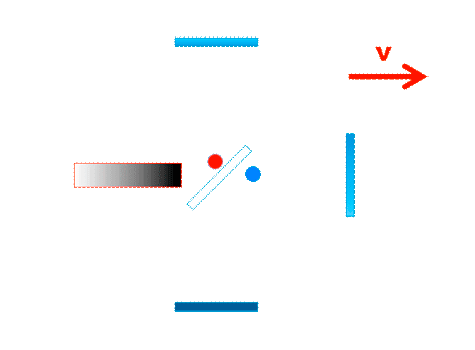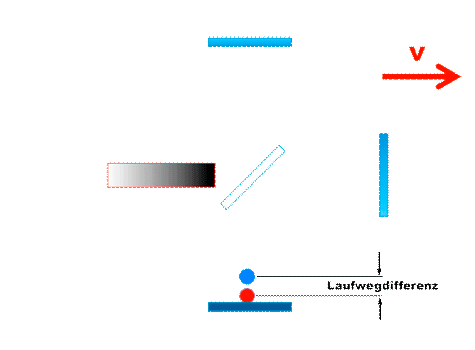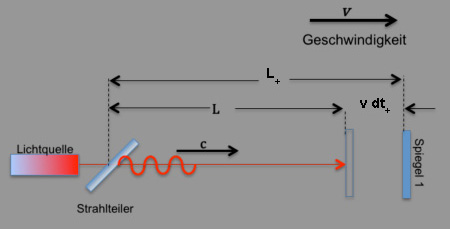
	Laufzeiteffekt in einem Arm des Michelson-Interferometers
	Auch für das ringförmige Sagnacinterferometer hatten wir angenommen, dass der Drehpunkt exakt im Zentrum des ringförmigen Lichtleitsystems liegt, so dass die Bewegung des Lichleiters immer exakt parallel zur Bewegungserichtung der Lichtwelle verläuft:
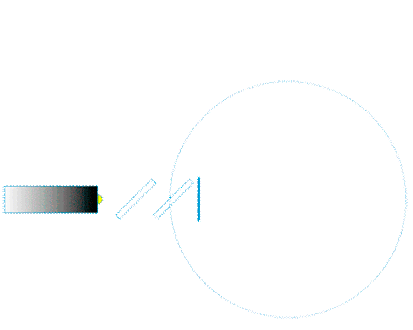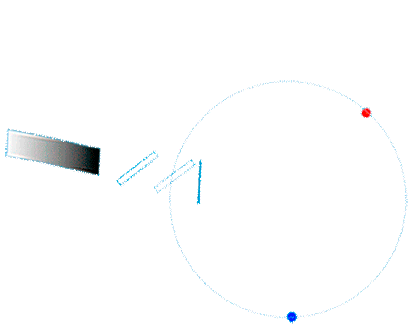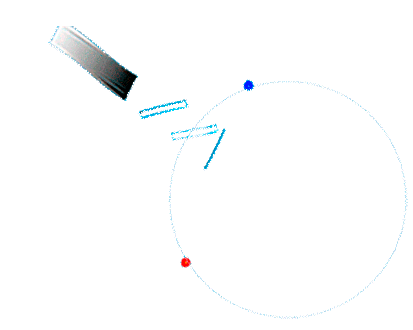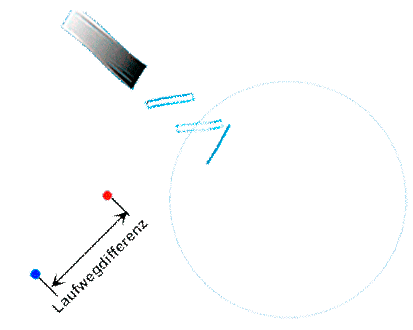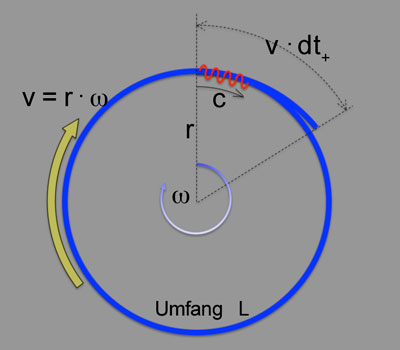
	Laufzeiteffekt im Sagnac-Interferometer in Drehrichtung
	Diese Spezialisierung auf eine bestimmte Konfiguration ist in der Literatur üblich, hat uns die Rechnung erleichert, aber vielleicht auch den Blick auf die eingangs formulierten Fragen verstellt die für die praktische Anwendung als Navigationssensor von großer Bedeutung sind. (Dezentraler Drehpunkt, Rolle der Signalgeschwindigkeit, u.s.w.)

	Also los ! Wie wollen wir es angehen?
	Die Grundidee ist die folgende: Wir berechnen die Laufzeit einer Lichtwelle z.B. in einer Glasfaser, während sich die Anordnung selbst in eine beliebige andere Richtung bewegt; z.B. so:



Startseite vorheriges Kapitel nächstes Kapitel

Oder anders ausgedrückt: Wir berechnen die Signallaufzeit für ein Strecken-element ds' und integrieren anschliessend über den gesamten Laufweg.	Uns interessiert dabei die Laufzeit des Signals sowohl für den für den Hin- als auch für den Rückweg ! Wir führen diese Rechnung zunächst nur für ein kleines Streckenelemente ds' durch. In einem späteren Schritt können wir diese Streckenelemente dann zu einem vollständigen Strahlverlauf zusammensetzen, - z.B. zu einem kreisförmigen wie beim Sagnacinterferometer. Aber für die Klärung einiger Grundsatzfragen wird das gar nicht nötig sein!

	Wir wollen die Situation 'mal etwas "mathematischer" darstellen:, damit wir anschliessend besser rechnen können. Die Pfeile (Vektoren) in der folgenden Skizze zeigen die Wegstrecken die der Lichtwellenzug mit der Geschwindigkeit c' (rot) und das Interferometer mit der Geschwindigkeit v (schwarz) in der Zeit dt' zurücklegen:
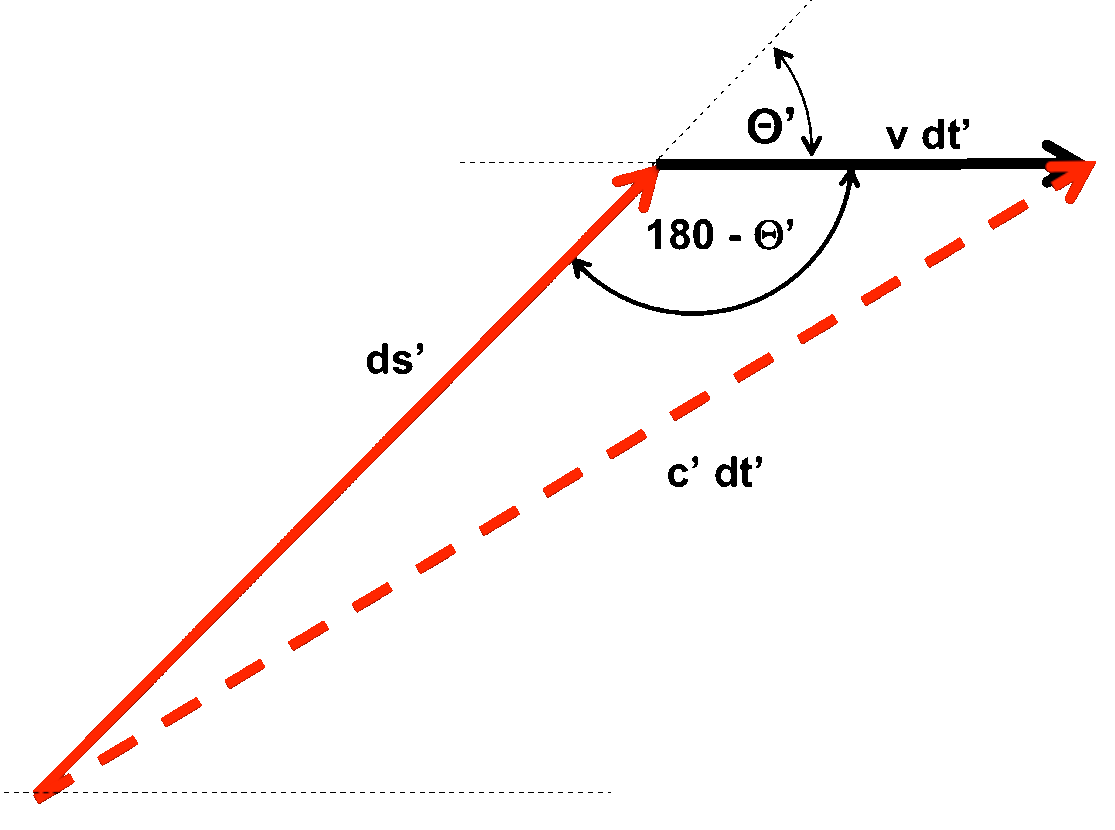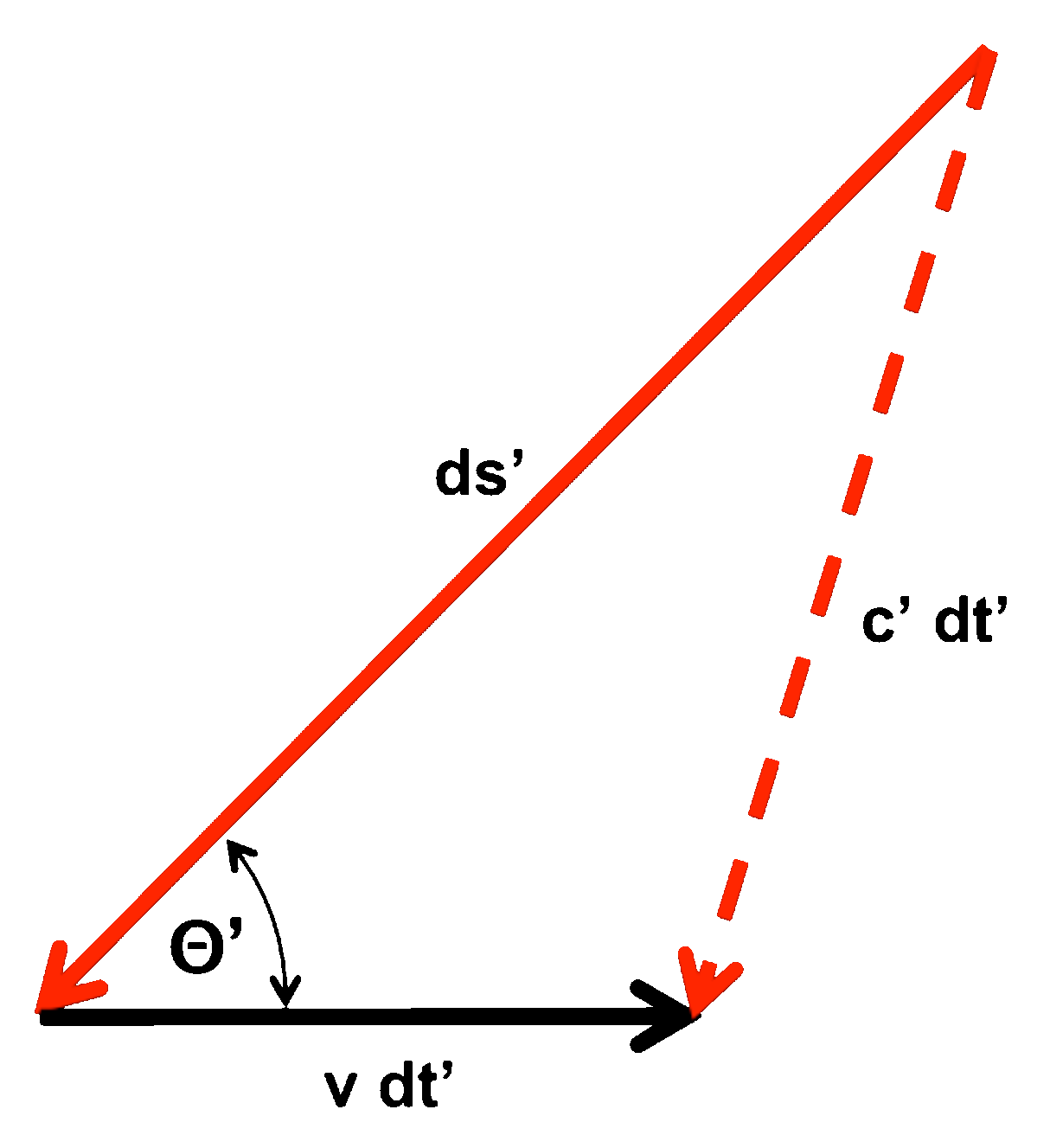
Wir verwenden hier "gestrichene Größen" (z.B. ds', dt',...), um deutlich zu machen, daß wir uns auf einen außerhalb des Systems ruhenden Beobachter beziehen, denn nur für diese Situation ist eine Laufweg- bzw. Laufzeitbetrachtuzng möglich! (Ein mit dem Messsystem mitbewegter Beobachter kann wegen des Relativitätsprinzips grundsätzlich keine gleichförmige Bewegung registrieren.)	Hinweg................................................................................ Rückweg
	Während die Lichtwelle das Wegstreckenelement ds' (rot) in der Zeit dt' durchläuft, wird das gesamte System (Interferometer) mit der Geschwindigkeit v um den Betrag vdt' (schwarz) verschoben. Der Winkel zwischen dem Wegstreckenelement und der äußeren Bewegungsrichtung ist Aus der Überlagerung dieser beiden Bewegungen ergibt sich die resultuierender Wegstrecke c'dt' (rot gestrichelt). Wir wollen nun für den Hinweg und den Rückweg die jeweiligen Signallaufzeiten berechnen, - zunächst für den "Hinweg" (linke Skizze oben).
Jetzt müssen wir etwas Trigonometrie bemühen - aber alles kein "Tiefsinn" ! Der COSINUSSATZ beschreibt die Beziehung zwischen den Seitenlängen und dem Cosinus eines Winkels in einem beliebigen Dreieck (s.u.) - z.B.: c² = a² + b² - 2ab cos(gamma) oder: a² = b² + c² - 2bc cos(alpha) oder: b² = a² + c² - 2ac cos (beta)	Nach dem Cosinussatz ergibt sich für den "Hinweg" die resultierende Wegstrecke c'dt'_hin und für den "Rückweg": (Dabei wurde die Beziehung benutzt !)
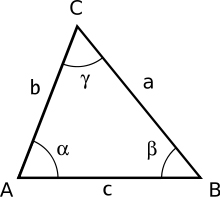
Quelle: Wikipedia	Diese Beziehungen werden wir nun dazu verwenden um die Signallaufzeiten für den Hinweg dt'_hin und für den Rückweg dt'_rückzu berechnen; dazu müssen wir die obigen quadratischen Gleichungen nur nach dt' _hin/rück auflösen. Hier das Ergebnis:
	Damit sind wir eigentlich schon fertig ! Mit diesen Laufzeiten dt'_hin/rück lassen sich nun die Effekte für das Michelson- und das Sagnac-Interferometer berechnen. Dazu ist folgendes zu bedenken: Beim Michelson-Interferometer läuft die Lichtwelle in jedem der beiden Interferometerarme hin und zurück. Die gesamte Laufzeit innerhalb eines Armes setzt sich also zusammen aus der Summe der Laufzeiten dt'_hin und dt'_rück_: dt'_Michelson= dt'_hin + dt'_rück
Startseite vorheriges Kapitel nächstes Kapitel	Beim Sagnac-Interferometer laufen die beiden Wellenzüge in entgegengesetzter Richtung durch das Ringinterferometer und der Messeffekt besteht in der Laufzeitdifferenz zwischen den beiden Wellenzügen: dt'_Sagnac = dt'_hin - dt'_rück
Zum Vergleich mit den Ergebnissen aus den vorhergehenden Kapiteln sollten wir 'mal kurz den Lichtwellenzug parallel zur äußeren Geschwindigkeit v legen, d.h. = 0 setzen. Dann erhalten wir für den Sagnaceffekt: und für den Michelsoneffekt: und das stimmt genau mit unseren früheren Ableitungen überein. Vergleichen Sie: Sagnac / Michelson (bitte anklicken!)	So, - mit diesem Rezept können wir nun die Laufzeiteffekte in beiden Interferometern bestimmen: und:
	Na gut, - das wußten wir ja alles schon! Und vor allem - wir haben immer noch keine Idee warum wir für das Michelsoninterferometer zwar einen Laufzeiteffekt ausrechnen können, obwohl er tatsächlich garnicht vorhanden ist und warum das beim Sagnacinterferometer funktioniert ? Um das - und alle die anderen Fragen, die ich oben gestellt habe - klären zu können, müssen wir noch einen Schritt weitergehen und die Tatsache ins Spiel bringen, dass wir mit den Experimenten als ruhender Beobachter einen Effekt in einem - relativ zu unserer Position - bewegten System messen möchten. Wir haben uns bislang auf den Standpunkt der klassischen Physik gestellt und vorausgesetzt, dass Geschwindigkeiten, Strecken und Zeitintervalle im bewegten System genau die gleichen sind wie im ruhenden. Als Ergebnis haben wir die Widersprüche zwischen Realität und Theorie erhalten, von den hier schon mehrfach die Rede war.

	Also nochmal von vorn ;-)
	Wir blicken aus dem "Beobachtersystem" (mit gestrichenen Größen) auf ein relativ zu unserer Position mit der Geschwindigkeit v bewegtes Messystem (mit ungestrichenen Größen) in dem das Experiment abläuft.
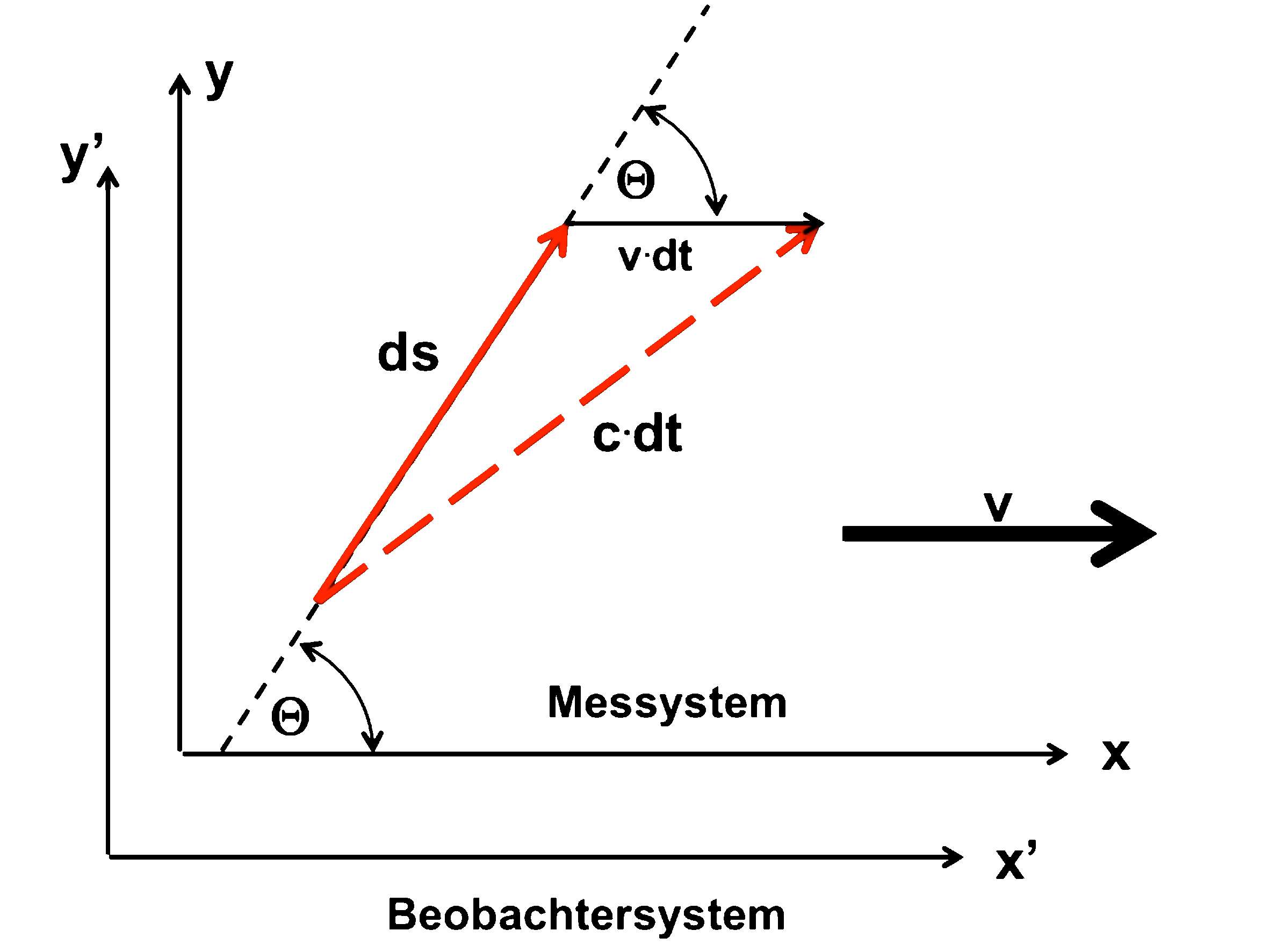Übrigens - niemand verbietet uns das Koordinatensystem so zu legen, dass unsere weiteren Rechnungen möglichst einfach werden; ich möchte deshalb die x-Achsen parallel zur Bewegungsrichtung v des Laufzeitexperimentes legen: ______________ (Achtung und bitte nicht verwechseln - die hier eingezeichneten (ungestrichenen !) Größen beziehen sich auf das mit der Geschwindigkeit v bewegte Messsystem !)
	Bei dieser Anordnung muß nun nach Ansicht von Herrn Einstein zwischen dem bewegten (x,y,z) und dem ruhenden Koordinatensystem (x', y', z') eine relativistische Korrektur berücksichtigt werden:
Ich plane ein weiteres Kapitel zur speziellen Relativitätstheorie, wo ich versuchen werde Ihnen diese und ähnliche Transformationen plausibel (nicht "verständlich") zu machen; bis dahin müssen Sie mir einfach glauben, oder in der einschlägigen Literatur nachblättern! _____________________________ Achtung - bitte nicht verwechseln: bei c₀ handelt es sich um dier Naturkonstante der Vakuumlicht-geschwindigkeit und nicht um die Signalgeschwindikeit c' bzw. c - obwohl die Signalgeschwindigkeit in einigen Fällen identisch mit c₀sein kann, müssen wir das streng unterscheiden	mit :
Startseite vorheriges Kapitel nächstes Kapitel	...alle anderen Koordinaten bleiben so wie sie sind. D.h. das Streckenelement ds' transformiert sich so:

	oder nach einigen Umformungen:
mit :
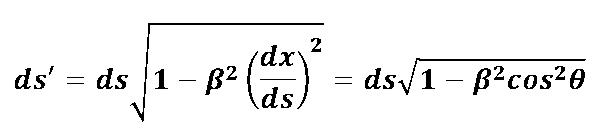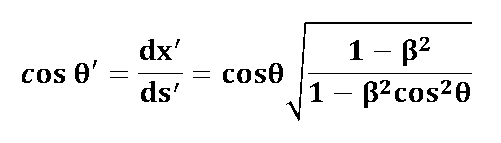	Für die Beziehung zwischen dem Winkel im bewegten System und dem Winkel im ruhenden System ergibt sich daraus:

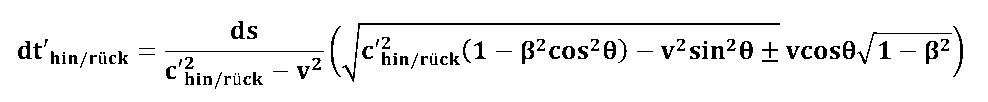	Wenn wir diese Ausdrücke für das Streckenelement ds' und in die obige Beziehung für die Signallaufzeiten dt'_hin/rück einsetzen, dann erhalten wir - nach "einigen" Umformungen:


	So, - fertig ! Was haben wir erreicht ? Wir sind jetzt in der Lage als ruhender Beobachter die Signallaufzeit in einem bewegten Messystem zu ermitteln! Keine Panik - wir werden in den nächsten Abschnitten den Ausdruck für die Signallaufzeiten dt'_hin/rück durch Einführung von Spezialfällen ganz erheblich vereinfachen und folgendes beweisen:
	- es gibt keinen Michelsoneffekt ! - die Signalgeschwindigkeit spielt für den Sagnaceffekt keine Rolle ! - gleichförmige Translationsbewegungen haben keinen Einfluss auf das Sagnac-Interferometer !
Startseite vorheriges Kapitel nächstes Kapitel