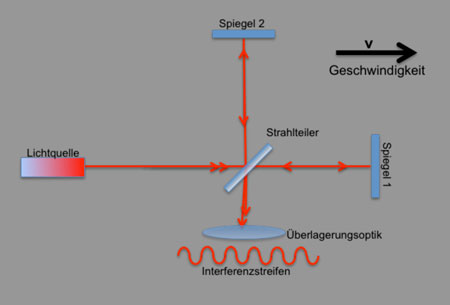
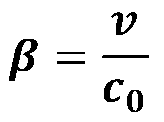| Laufzeiteffekte in relativ bewegten Systemen - "Sagnac" bleibt erhalten - "Michelson" verschwindet ! | |
|
|
|
| Startseite vorheriges Kapitel nächstes Kapitel |
Wir haben im Kapitel "Laufzeiteffekte in relativ bewegten Systemen - Vorüberlegungen" eine Formel hergeleitet, die es uns erlaubt die Laufzeit eines (Licht-)Signals über ein Wegstreckenelement ds zu berechnen.
Sie erinnern sich ? (Hier können Sie alles auch noch einmal nachlesen ! ) |
| mit:
dt' - Signallaufzeit im Wegstreckenelement ds |
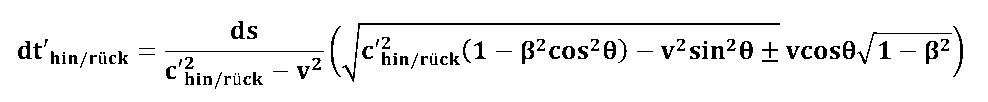 Die "gestrichenen" Größen beziehen sich auf das ruhende Beobachtersystem; ungestrichene Gößen beziehen sich auf das bewegte Messystem. |
|
"Hinweg"...................................................................."Rückweg" |
|
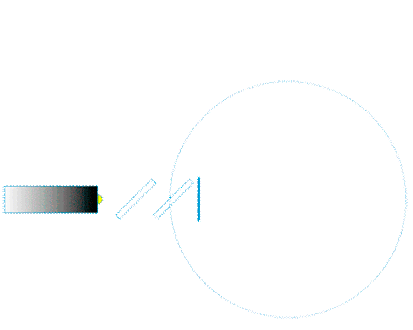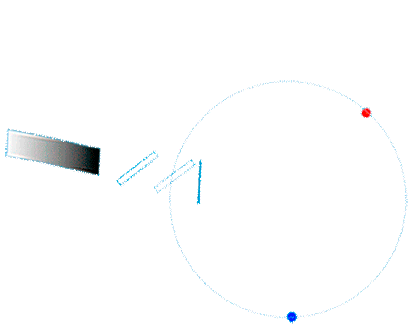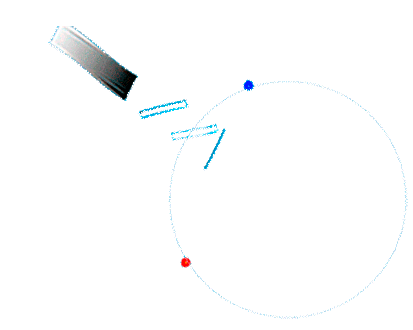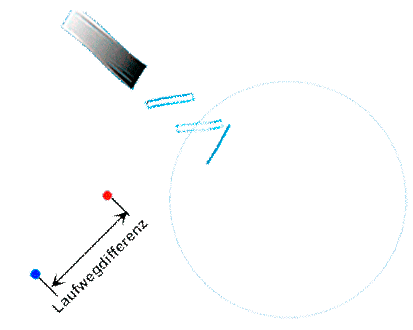 Sagnac-Messprinzip: Laufzeitdifferenz |
Mit dieser Formel sollte es jetzt möglich sein, die am Sagnac- und am Michelson-Interferometer beobachteten Effekte widerspruchsfrei zu beschreiben.
Für die im Sagnac-Interferometer gegensinnig umlaufenden Wellenzüge ergibt sich der Messeffekt aus der Differenz der Laufzeiten für Hin- und Rückweg. (mehr dazu hier.) dt'Sagnac = dt'hin - dt'rück |
|
|
|
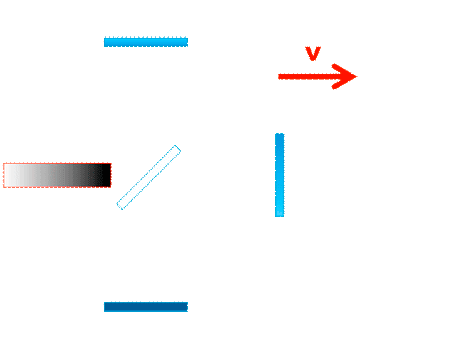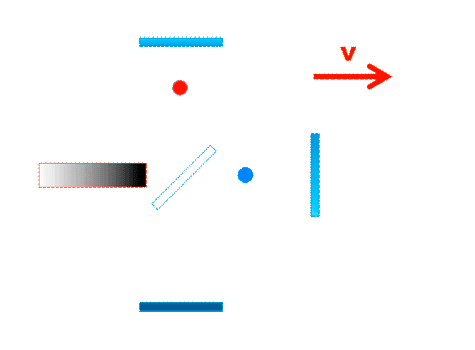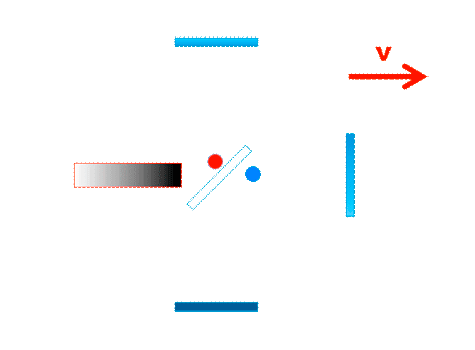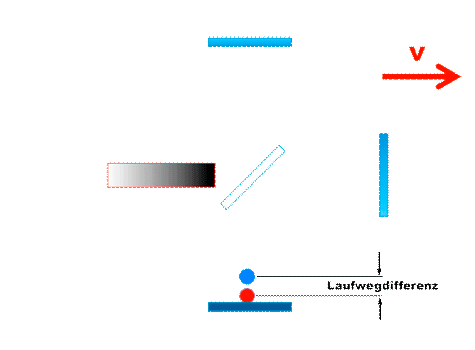 Michelson-Messprinzip: Laufzeitsumme in den Interferometerarm /Laufzeitdifferenz zw. den Armen. |
Für das Michelson-Inferometer müssen wir in jedem der beiden Arme jeweils die Summe der Laufzeiten für Hin- und Rückweg bilden: (mehr dazu hier) und anschliessend die Laufzeiten in beiden Interferometerarmen vergleichen:
dt'Michelson = dt'hin + dt'rück |
|
|
|
| Berechnung des Laufzeiteffektes im Sagnac-Interferomerter | |
| Bevor wir die Signallaufzeit für das Sagnac-Interferometer berechnen sollten wir die die Ausrücke für die beiden gegensinnig umlaufenden Wellenzüge ("hin" und "rück") nocheinmal notieren. | |
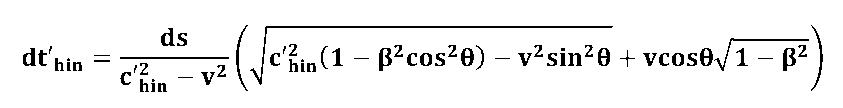
|
|
| Die Signalgeschwindigkeiten c'hin und c'rück können durchaus unterschiedlich sein. Aus der Sicht der vorrelativistischen Physik würde man in einem bewegten Medium eine "Fresnel-Mitführung" erwarten. Im Vakuum könnte man für beide Lichtwellenzüge mit derselben Geschwindigkeit c0 rechnen.
Wir werden in einem späteren Kapitel ("Einfluß der Signalgeschwindigkeit") untersuchen, in welcher Weise unterschiedliche Signalgeschwindigkeiten c'hin und c'rück den Effekt beeinflussen; hier wollen wir zunächst annehmen, dass die beiden Signalgeschwindigkeiten identisch mit der Vakuumlichtgeschwindigkeit c0 sind. c'hin = c'rück = c0 |
|
| Unter dieser Voraussetzung erhalten wir für den Sagnac-Laufzeiteffekt:
|
|
| Im Kapitel "Einfluß eines dezentralen Systemdrehpunktes" werden wir die Frage untersuchen in welcher Weise der Winkel Um den Anschluß an die übliche Formulierung des Sagnaceffektes zu gewinnen, wollen wir hier aber zusätzlich annehmen, daß das Sagnac-Interferometer exakt ringförmig ist und sich um einen zentralen Drehpunkt dreht (s.d. die obige Skizze/Animation!). D.h. der Lichtwellenzug verläuft exakt parallel zur (Dreh-)Bewegung des Lichtführungssystems, d.h.
|
|
| Jetzt ergibt sich für die Laufwegdifferenz:
|
|
F = Interferometerfläche; c0 = Vakuumlichtgeschwindigkeit; |
... und unter Berücksichtigung von
|
| Ganz offensichtlich liefert die obige Formel für den Laufzeiteffekt in relativ bewegten Systemen das richtige Ergebnis für das Sagnac-Interferometer, - zumindest für die in der Literatur durchweg benutzten Spezialfälle eines ringförmigen Interferometers mit zentralem Drehpunkt und der Vakuumlichtgeschwindigkeit c0. | |
|
|
|
| Berechnung des Laufzeiteffektes im Michelson-Interferometer | |
| Details zu Michelson-Interferometer können Sie hier nachlesen. | |
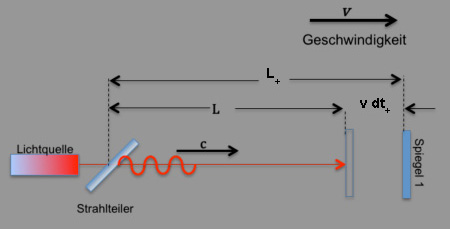
| Hier noch einmal die Prinzipskizze für einen Arm des Michelson-Interferometers: | |
 |
|
|
|
|
| Zunächst 'mal werden wir die obige Formel für die Signallaufzeit etwas vereinfachen, ohne dabei die Allgemeingültigkeit einzuschränken. Da wir ein Laufzeitexperiment mit einem Lichtstrahl vorhaben, setzen wir als Signalgeschwindigkeit c' für den Hin- und Rückweg die Vakuumlichtgeschwindigkeit c0 an ! | |
| Startseite vorheriges Kapitel nächstes Kapitel |
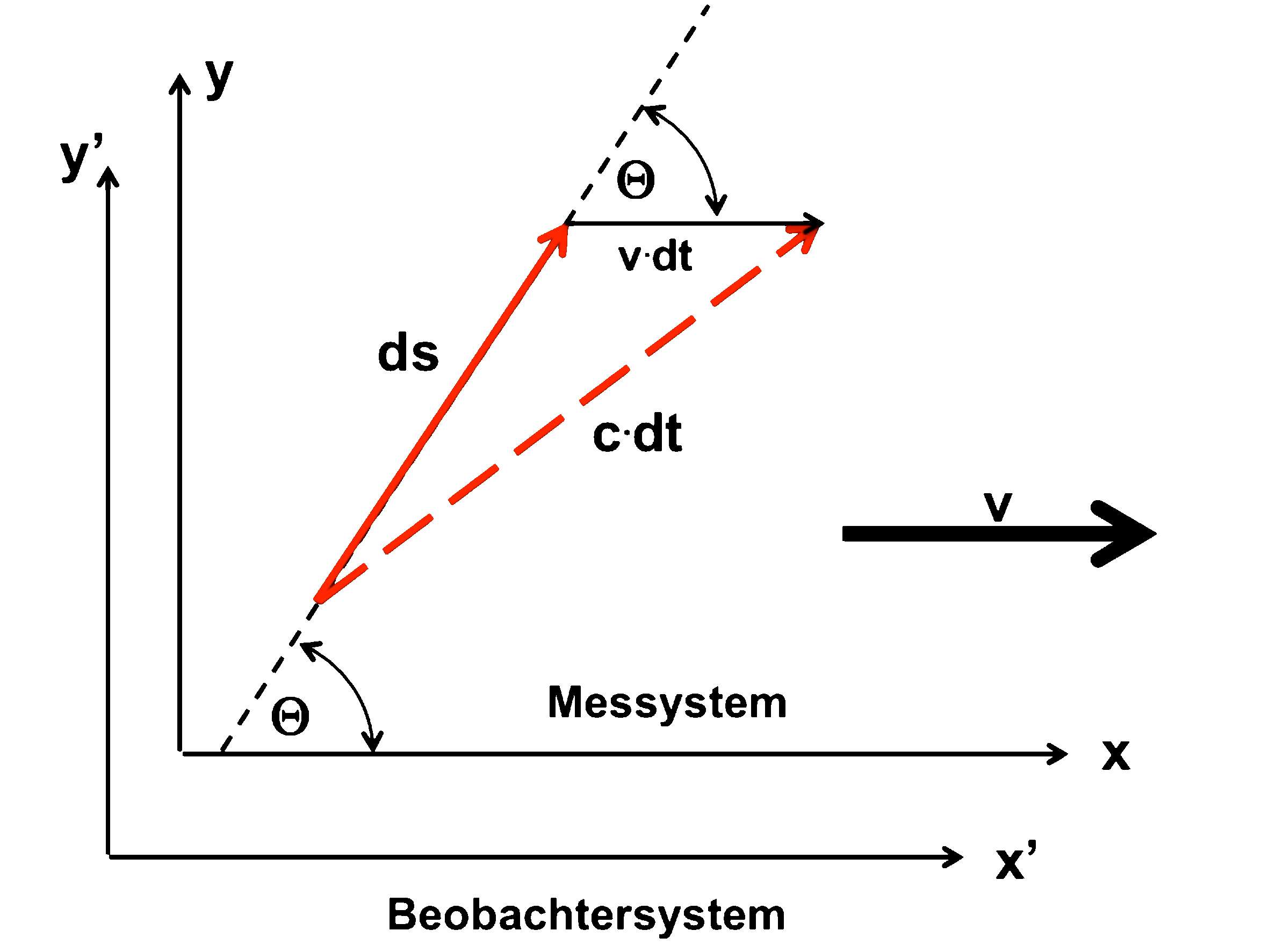
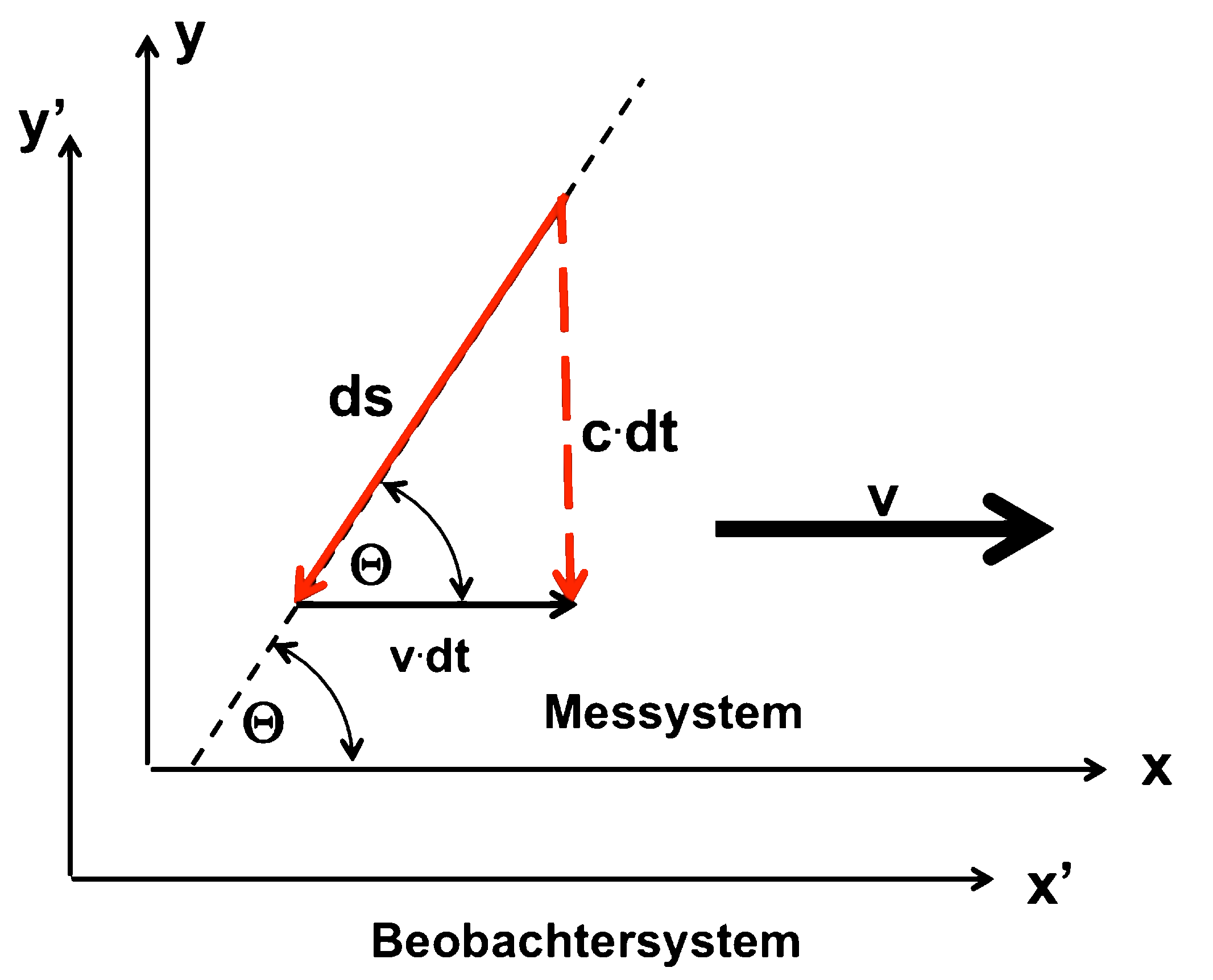
Als Laufzeit für den Hinweg ergibt sich mit c' = c0 aus der obigen Formel:
|
| Und für den Rückweg gilt:
|
|
|
|
In einem Michelsoninterferometer müssen wir nun die Laufzeiten für Hin- und Rückweg addieren (mehr dazu), d.h. wir erhalten für die Gesamtlaufzeit in einem Interferometerarm,
dt'Michelson = dt'hin + dt'rück bzw.:
|
 |
Merken Sie was ?
Der Ausdruck für die Laufzeit dt'Michelson ( Hinweg + Rückweg !) enthält nicht mehr den Winkel |
|
|
|
 |
Wir haben hier die Laufzeit (hin und zurück) in einem Arm des Michelson-Interferometers diskutiert. Tatsächlich besteht das Michelson-Interfereometer aber aus zwei zueinander senkrechte Armen. Der erwartete Effekt sollte sich dann aus dem Vergleich der Laufzeiten in den beiden Armen ergeben, nachdem das Interferometer um 90° gedreht wurde. Wenn aber - wie hier gezeigt - die Laufzeit in den beiden Armen des Interferometers sich bei Drehung nicht ändert , dann kann auch der Vergleich der Laufzeiten aus beiden Armen keinen Effekt ergeben.
|
| Startseite vorheriges Kapitel nächstes Kapitel |
|
|
|
|
| Wir haben jetzt also Klarheit was die unterschiedlichen Ergebnisse des Sagnac- und des Michelson-Experiments betrifft:
Wenn bei der Berechnung der Signallaufzeiten in relativ bewegten Systemen relativitische Korrekturen zwischen dem ruhenden-/ Beobachter-System und dem bewegten Messsystem berücksichtigt werden , dann sind - im Gegensatz zur klassischen Rechnung - Theorie und Praxis in perfekter Übereinstimmung: |
|
| Das Michelson-Interferometer zeigt keinen Effekt, das Sagnac-Interfereometer zeigt einen Laufzeiteffekt proportional zur Drehgeschwindigkeit ! | |

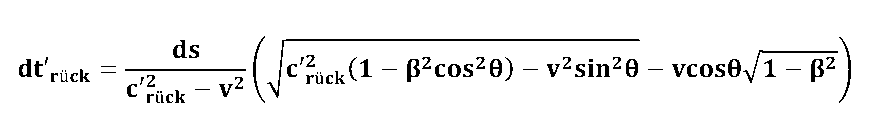
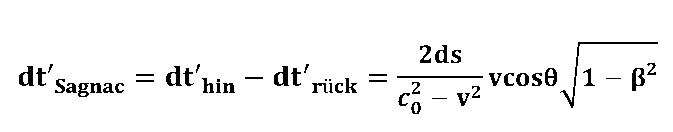
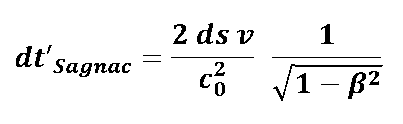

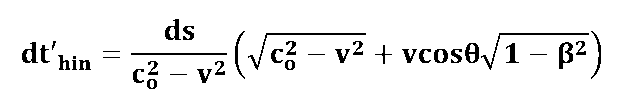

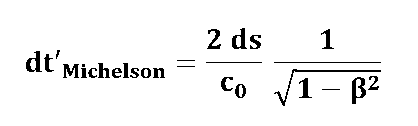 mit
mit