| Laufzeiteffekte in relativ bewegten Systemen - Einfluß der Signalgeschwindigkeit auf den Sagnaceffekt | |
| oder: Ist der Sagnaceffekt ein relativistischer Effekt ? | |
|
|
|
| Startseite vorheriges Kapitel nächstes Kapitel |
Ein Sagnac-Interferometer kann auf sehr unterschiedliche Weise aufgebaut sein, - aber grundsätzlich wird immer ein in sich geschlossenes Führungssystem für das Signal, bzw. die Lichtwellen benötigt Dieses kann mit Umlenkspiegeln, Prismen oder Lichtwellenleitern bzw. Glasfasern realisiert werden. Insbesondere der "Glasfaserkreisel" hat eine große praktische Bedeutung und es ist deshalb auch von Interesse in welcher Weise der temperaturabhängige Brechungsindex bzw. die Signalgeschwindigkeit den Messeffekt beeinflußt. Etwas salopp formuliert - wenn sich herausstellen sollte, daß der Messeffekt des "Faserkreisels" von der Lichtgeschwindigkeit bzw. vom Brechungsindex abhängt und damit temperaturempfindlich ist, dann haben wir ein Problem ! Na, dann wollen wir 'mal sehen: |
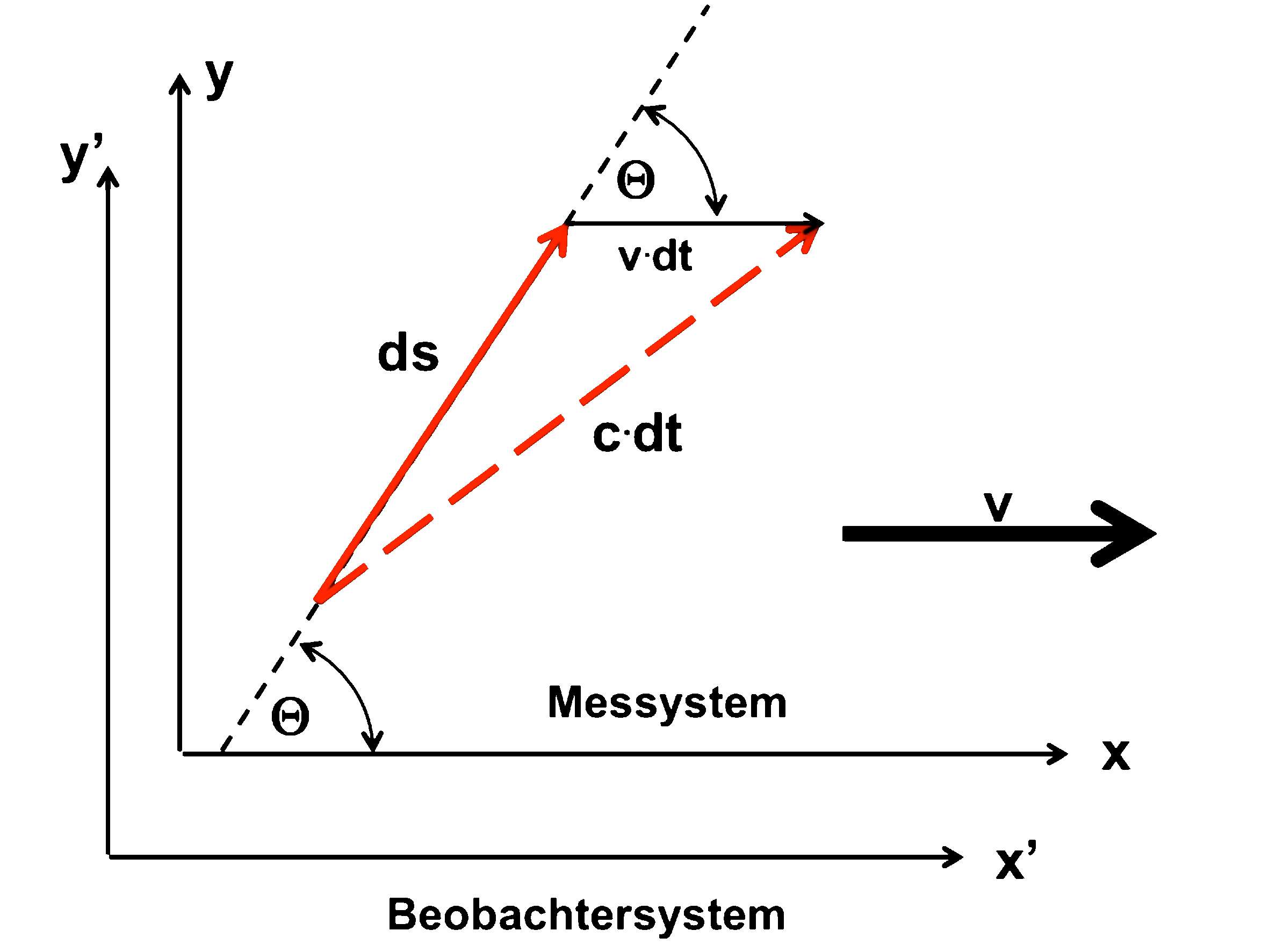
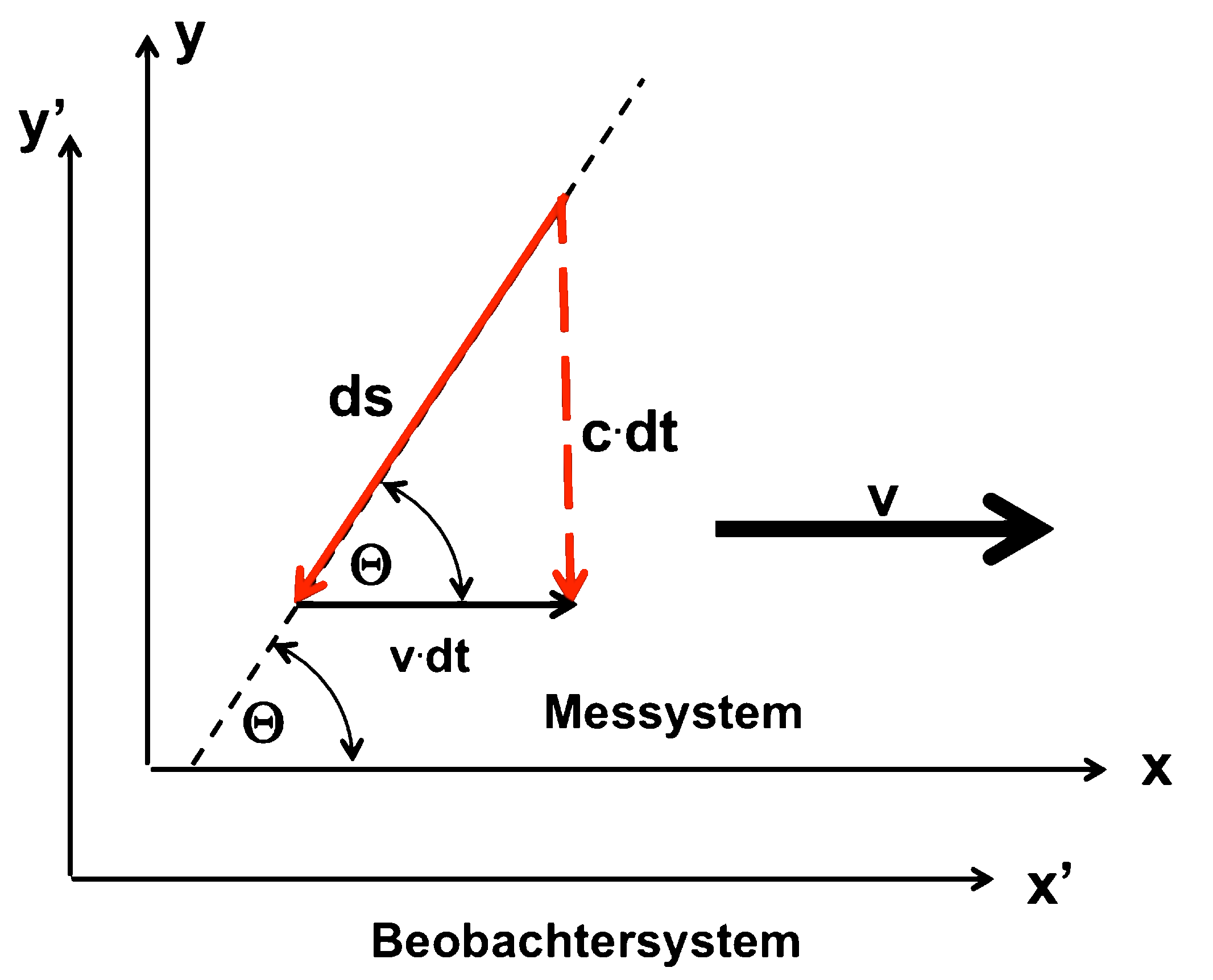
| Wir haben im Kapitel "Laufzeiteffekte in relativ bewegten Systemen - Vorüberlegungen" eine Formel hergeleitet, die es uns erlaubt die Laufzeit eines (Licht-)Signals über ein Wegstreckenelement ds zu berechnen. | |
| mit:
dt' - Signallaufzeit im Wegstreckenelement ds |
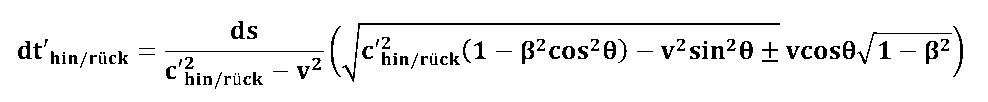 Die "gestrichenen" Größen beziehen sich auf das ruhende Beobachtersystem; ungestrichene Gößen beziehen sich auf das bewegte Messystem. Sie erinnern sich ? (Hier können Sie das alles auch noch einmal nachlesen ! ) |
|
"Hinweg"...................................................................."Rückweg" |
|
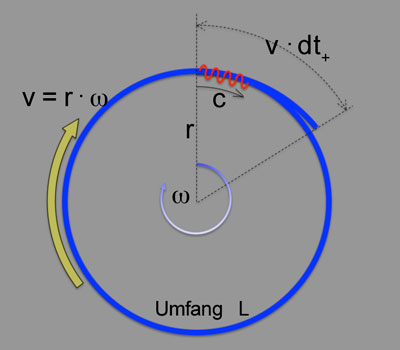 |
Und weil wir uns das Leben immer so einfach wie möglich machen wollen, nehmen wir in diesem Fall an, dass es sich um einen kreisförmigen Aufbau handelt und der Drehpunkt exakt im Zentrum liegt.
Für unsere Frage welchen Einfluß die Signal-/Lichtgeschwindigkeit auf den Messeffekt hat, ist das keine Einschränkung der Allgemeingültigkeit ! Mit dieser Vereinfachung ( |
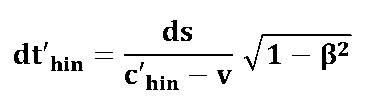 |
|
| ... und für das entgegengesetzt umlaufende Signal: | |
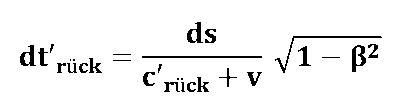 |
|
| Startseite vorheriges Kapitel nächstes Kapitel |
Für die jeweiligen Signalgeschwindigkeiten c'hin/rück müssen wir bedenken, dass sich alles in einem relativ zum Beobachter bewegten Messystem abspielt, das sich mit der (Tangential)-Geschwindigkeit v bewegt. D.h. wir müssen das relativistische Additionstheorem für Geschwindigkeiten anwenden: |
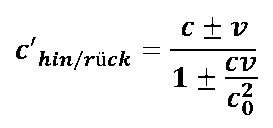 |
|
| wobei c die Signalgeschwindigkeit im ruhenden System und c0 die Vakuumlichtgeschwindigkeit als Naturkonstante ist! | |
| Wenn man damit nun die (Sagnac-)Laufzeitdifferenz dt'Sagnac = dt'hin - dt'rück berechnet, dann erhält man den etwas "sperrigen" Ausdruck ... | |
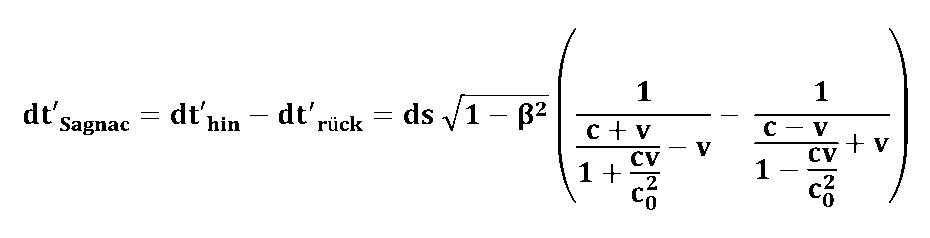 |
|
| ... der sich aber nach einer Zusammenfassung der vielen Brüche "in Wohlgefallen" auflöst: | |
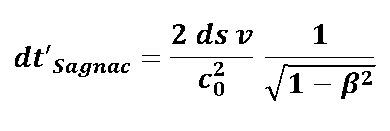 |
|
| und mit |
|
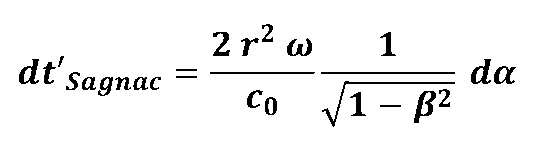 |
|
Integriet man diesen Ausdruck über einen vollen Umlauf 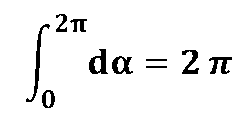 und berücksichtigt |
|
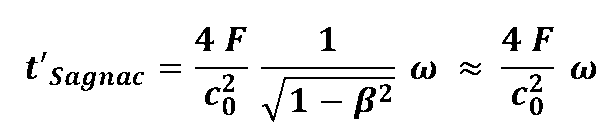 |
|
| Startseite vorheriges Kapitel nächstes Kapitel |
... eine Beziehung die uns bestens bekannt ist !
Schauen Sie mal zum Vergleich in das Kapitel "Sagnac" ! |
| .
Und jetzt ? Wozu der ganze Aufwand, wenn die klassische Rechnung scheinbar das gleiche Ergebnis liefert? |
|
 |
Kann ich Ihnen sagen!
Im Gegensatz zur klassischen Herleitung können wir jetzt klar erkennen, daß die Formel für die Sagnac-Laufzeitdifferenz die Signalgeschwindigkeit c überhaupt nicht mehr enthält, sondern nur noch die Naturkonstante c0 (Vakuumlichtgeschwindigkeit) ! Das ist wirklich eine Sensation, die zwei wichtige Konsequenzen hat - eine praktische und eine theoretische: Zunächst die praktische: Phasengeschwindigkeit, Brechungsindex und Dispersion spielen keine Rolle mehr. Als möglicher Fehlereinfluß bleibt nur noch eine Schwankung der Interferometergeometrie, bzw. der Fläche F und die sollte sich durch Verwendung entsprechender temperaturunempfindlicher Materialien recht gut stabilisieren lassen! |
| . | |
|
(... finde ich fast noch spannender !)
|
Und nun die "theoretische Konsequenz": |
| *) Ein "Schallwellen-Ringinterferometer" ist praktisch wohl kaum realisierbar, - aber das soll uns im Augenblick nicht weiter stören! |
Auch wenn Ihnen der Unterschied nicht aufgefallen sein sollte, - wir haben jetzt zwei Formeln zur Berechnung des Sagnaceffektes, die zwar sehr ähnlich aussehen, die aber unterschiedlicher nicht sein könnten:
... blättern Sie nochmal zurück! Das die zuletzt hergeleitete Formel für t'Sagnac-relativistisch nicht mehr die Signalgeschwindigkeit c sondern die Vakuumlichgeschwindigkeit c0 als Naturkonstante enthält, ist natürlich ein Ergebnis der Tastsache, dass wir für die Signalgeschwindigkeit das relativistische Additionstheorem
benutzt haben ! Verblüffend bleibt trotzdem, dass die Signalgeschwindigkeit c nicht mehr auftaucht! Das bedeutet doch, daß der Sagnaceffekt z.B. auch für Schallwellen existiert. *) |
|
Die Gegner der Relativitätstheorie - z.B. der Nobelpreisträger Philip Lenard - beziehen die Argumente für ihre Kritik an der Relativitätstheorie u.a. aus der Tatsache, dass sich der Wert der Laufzeitdifferenz beim Sagnanaceffekt auch sehr gut mit den Mitteln der klassischen Physik berechnen lässt. Jetzt zeigt sich aber, daß diese Übereinstimmung zwischen klassischer und relativitischer Physik nur ein Zufall war, denn bei allen bekannten Sagnacexperimenten wurde als Signal eine Lichtwelle benutzt, deren Geschwindigkeit c sehr dicht an der Vakuumlichtgeschwindigkeit c0 lag. Mit der damals verfügbaren Messgenauigkeit konnte bei der Auswertung der Ergebnisse dazwischen nicht unterschieden werden Mit den heutigen technischen Möglichkeiten sollte es aber möglich sein zu entscheiden, welcher Ansatz der richtige ist - der relativistische oder der klassische. Dieses Experiment wurde 1979 von Leeb, Schiffner und Scheiterer mit einem Glasfaser-Ringinterferometer tatsächlich auch gemacht! |
|
| W.R. Leeb, G. Schiffner, E. Scheiterer, "Optical fiber gyroscope: Sagnac or Fizeau effect?", Applied optics, Vol 18, No.9 (1979), pp-1292-1295 |
Die Grundidee des Experimentes von Leeb/ Schiffner/Scheiterer bestand darin, den ringförmigen Glasfaserlaufweg einerseits und die Baugruppe bestehend aus Lichtquelle und der Auslese- bzw. Überlagerungsoptik durch flexible Lichtleitfasern so zu verbinden, so dass diese Baugruppe mal mit dem rotierenden Lichtwellenleiter mitbewegt werden konnte und ein anderes mal relativ zum rotierenden Lichtwellenleiter ruhte. Insbesondere im letzteren Fall (Ausleseoptik ruhend, Glasfaserring rotierernd) ist aus der Sicht der klassischen / vorrelativistischen Physik damit zu rechnen, dass sich eine Mitführung des Lichtes im bewegten Medium ereignet. (Fresnel-Mitführung; s.d. A. Sommerfeld, "Vorlesung über theoretische Physik", Bd.IV, S. 58), was zu einer geänderten Lichtgeschwindigkeit c'hin/rück führt: |
| Startseite vorheriges Kapitel nächstes Kapitel |
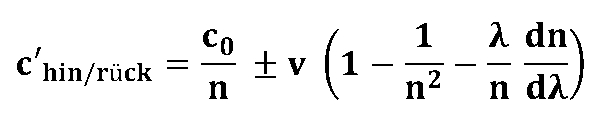 |
| Wenn man mit diesem Ausdruck für die Signalgeschwindigkeit c'hin/rück in die Formel für den Sagnaceffekt eingeht und über einen vollen Umlauf integriert, dann sollte sich für die Laufzeitdifferenz t'Sagnac der folgende Zusammenhang ergeben: | |
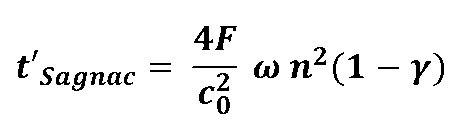 |
|
| wobei |
|
| Wie gesagt - nach den Prinzipien der vorrelativistischen Physik müßte der Sagnaceffekt über den Mitführkoeffizienten von den Materialeigenschaften des lichtführenden Mediums abhängen.
In Ihrem 1979 durchgeführten Experiment konnten Leeb, Schiffner und Scheiterer aber zeigen, dass das eindeutig nicht der Fall ist ! Daraus folgt: der Sagnaceffekt ist unabhängig von der Signalgeschwindigkeit **) und das wiederum ist nur verständlich vor dem Hintergrund der Relativitätstheorie ! Fazit: der Sagnac ist ein relativistischer Effekt! |
|
|
|
|
| Startseite vorheriges Kapitel nächstes Kapitel |
**) Fragen Sie doch mal einen der vielen Einsteinkritiker (z.B.hier) wie sie diese Tatsache ohne Rückgriff auf die Relativitätstheorie erklären!
Ich gebe zu, - die spezielle Relativitätstheorie (SRT) ist eine arge Zumutung für unsere Vorstellungskraft und wenn man "Anschaulichkeit" zum Maßstab für die Richtigkeit einer wissenschaftlichen Aussage macht, so wie der Nobelpreisträger Philipp Lenard (Initiator einer "arischen Physik") , dann hat man tatsächlich ein Problem. Das ändert aber nichts an der Tatsache, dass die SRT als einzige eine widerspruchsfreie Erklärung sämtlicher Effekte rund um die Lichtausbreitung in relativ bewegten Systemen liefert ! |

 und
und 